Μαθηματικά Γ - 4ος

4 / 80

1ο Κεφάλαιο – Συναρτιςεισ
480
Απόδειξη
Υποκζτουμε ότι υπάρχουν 1 2 x ,x Δ με 1 2 x x τζτοια ϊςτε  1 f x
και  2 f x να είναι ετερόςθμοι αρικμοί. Τότε επειδι θ f είναι
ςυνεχισ ςτο  
1 2 x ,x Δ με    1 2 f x f x 0  κα υπάρχει  
1 2 ξ x ,x
τζτοιο ϊςτε   f ξ 0 , άτοπο γιατί   f x 0 ςτο Δ. Δθλαδι θ f
διατθρεί το πρόςθμό τθσ ςτο Δ.
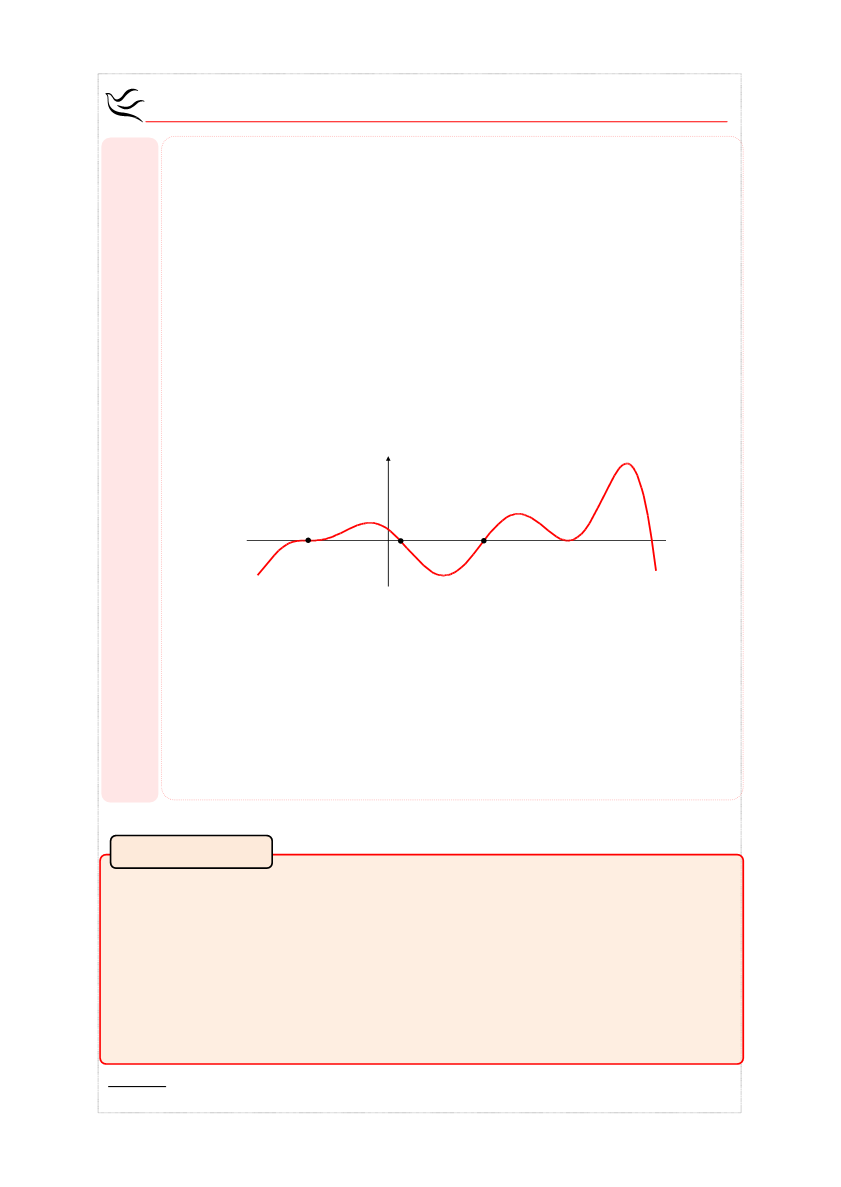
 Μια ςυνεχισ ςυνάρτθςθ f διατθρεί πρόςθμο ςε κακζνα από το
διαςτιματα ςτα οποία οι διαδοχικζσ ρίηεσ τθσ f χωρίηουν το πεδίο
οριςμοφ τθσ.
x
y
ρ5 ρ4 ρ3 ρ2 ρ1
(+)
( )
(+)
()
(+)
Ζτςι μποροφμε να προςδιορίςουμε το πρόςθμο τθσ f για τισ
διάφορεσ τιμζσ του x ωσ εξισ:
 Βρίςκουμε τισ ρίηεσ τθσ f.
 Σε κακζνα από τα υποδιαςτιματα που ορίηουν οι διαδοχικζσ
ρίηεσ, επιλζγουμε ζναν αρικμό και βρίςκουμε τθν τιμι τθσ f
για αυτόν τον αρικμό. Το πρόςθμο αυτισ τθσ τιμισ είναι και το
πρόςθμο τθσ f ςτο αντίςτοιχο διάςτθμα.
Παρατηρήςεισ
 Το αντίςτροφο του κεωριματοσ Bolzano δεν ιςχφει. Υπάρχει δθλαδι
ςυνάρτθςθ f όπου:
 είναι ςυνεχισ ςτο  α,β με ρίηα ςτο  α,β χωρίσ όμωσ να ιςχφει
    f α f β 0  .
 ζχει ρίηα ςτο  α,β , ιςχφει     f α f β 0  αλλά δεν είναι ςυνεχισ ςτο
 α,β .
Σχόλια