Μαθηματικά Γ - 4ος

6 / 80

1ο Κεφάλαιο – Συναρτιςεισ
482
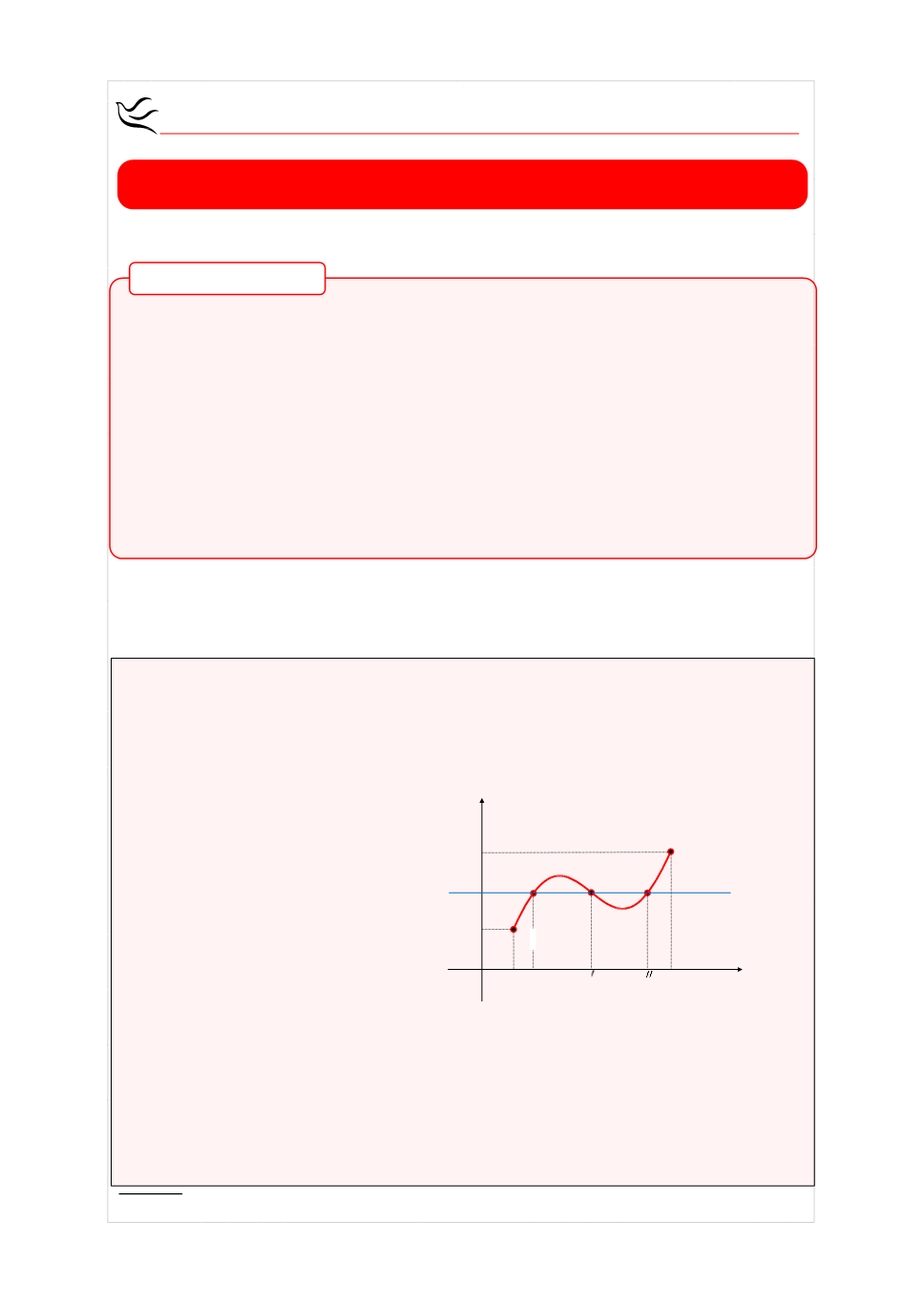
Θεώρημα
Ζςτω μια ςυνάρτθςθ f, θ οποία είναι οριςμζνθ ςε ζνα κλειςτό διάςτθμα  α,β
Αν:
 θ f είναι ςυνεχισ ςτο  α,β και
     f α f β
τότε, για κάκε αρικμό θ μεταξφ των   f α και   f β υπάρχει ζνασ, τουλάχιςτον
 
0 x α,β τζτοιοσ, ϊςτε  0 f x θ .
Απόδειξη
Ασ υποκζςουμε ότι     f α f β . Τότε κα ιςχφει     f α θ f β  . Αν κεωριςουμε
τθ ςυνάρτθςθ     g x f x θ  ,   x α,β , παρατθροφμε ότι:
 θ g είναι ςυνεχισ ςτο  α,β και
     g α g β 0 ,
Αφοφ
    g α f α θ 0  
    g β f β θ 0   .
Επομζνωσ, ςφμφωνα με το κεϊρθμα του Bolzano, υπάρχει  
0 x α,β τζτοιο,
ϊςτε    0 0 g x f x θ 0   , οπότε  0 f x θ .
0 x
0 x 0 x
y
B(β,f (β))
f (α)
f (β)
O β
y=θ
θ
α x
Α(α,f (α))
Θεώρημα ενδιάμεςων τιμών (Darboux 1842- 1917)